ACM_Algorithm

线段树笔记

文章目录
  1. 1. 简介
  2. 2. 单点更新，区间查询
  3. 3. 区间更新，单点查询
  4. 4. 区间更新，区间查询
  5. 5. 区间最值模板
  6. 6. 参考

有这样一类问题，给定一个数列，让你求某段区间内和。如果对某个值或某段区间内的值进行修改后，如何快速的求和。如果线性执行更新操作或求和操作，无疑时间复杂度太大了。
那么借助分治的思想，在执行更新区间的操作时，把它转化为几段区间的更新，同样求和操作时，也通过维护分段区间的和来达到快速求区间和的问题。线段树就是利用二叉树这种数据结构，来维护区间信息的一种数据结构。

简介

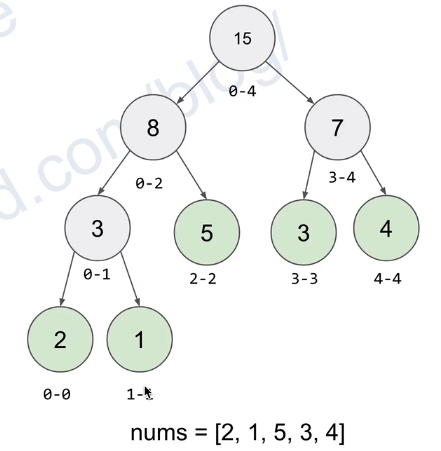
segment tree

  • 二叉树的每个结点，都代表一段区间。考虑到二叉树的结构，他的根结点就维护从1~n这段区间的信息，根结点的左子树维护1~mid这段区间，右子树维护mid+1~n这段区间，以此递归向下。
  • 一般每个结点需要维护区间修改的信息，以及区间和的信息。
  • 二叉树的叶子结点(从左到右)储存数列的1~n。
    修改操作分为两类，一种是在区间的原数值基础上进行修改：加或减去val、乘以val、开根号、、、等；一种是将该区间的值改为val；不同的操作在维护区间和时，相应的有些变化。下面以区间和问题为例，对线段树的实现进行讲解。
    如果实现线段树一般需要以下几种操作：
    1
    2
    3
    build(start,end,vals)	//o(n)
    update(index,value)	//o(logn)
    rangeQuery(start,end)	//o(logn+k)

另外线段树可以用结构体指针来索引左右孩子，也可以用数组来存储(申请的长度至少要4n)，本文选用前者。

单点更新，区间查询

  • 307.Range Sum Query - Mutable
    如果做过一些二叉树递归类的题，这个应该就挺好理解了。
    几年前我尝试学习线段树的时候，感觉好难。后来刷了一些二叉树类的题，现在再来学习线段树，发现还是挺好理解的。所以如果有些算法学起来困难，可能是前置知识的掌握还不到位。
    二叉树的每个结点需要用start、end存储线段起止号，sum存储该段区间的和，另外left、right索引左右子树。
    建树过程用buildTree()递归创建就好了，从根节点开始创建，终止条件是线段的start==end(到达叶子节点了，从左到右看就是原数列)。
    单点更新：由于是单点更新，所以一定会从根节点往下找，直到相应的叶子节点。然后更新叶子节点。最后还要在回溯的过程中更新每一个包涵该点的线段。
    区间查询：对于要查询的区间，如果都被包涵在左子树，就去左子树查询；如果被包涵在右子树，就去右子树查询；如果要查询的区间在左右子树标示的线段中都有一部分，那就分别将左右子树查询的结果加起来。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    //线段树是利用二分思想解决区间问题
    class SegmentTreeNode{
    public:
        SegmentTreeNode(int start,int end,int sum,
                        SegmentTreeNode *left=nullptr,SegmentTreeNode *right=nullptr):
                start(start),end(end),sum(sum),left(left),right(right) {}
        //禁用赋值构造和拷贝构造函数
        SegmentTreeNode(const SegmentTreeNode&)=delete;
        SegmentTreeNode& operator=(const SegmentTreeNode&)=delete;
        ~SegmentTreeNode(){
            delete left;
            delete right;
            left=right=nullptr;
        }
    public:
        int start;
        int end;
        int sum; //可以是max，min
        SegmentTreeNode *left;
        SegmentTreeNode *right;
    }; //end class SegmentTreeNode

    class NumArray {
    public:
        NumArray(vector<int>& nums) {
            nums_.swap(nums);
            if(!nums_.empty()){
                root_.reset(buildTree(0,nums_.size()-1));
            }
        }
        void update(int i, int val) {
            updateTree(root_.get(),i,val-nums_[i]);
        }
        int sumRange(int i, int j) {
            return sumRange(root_.get(),i,j);
        }
    private:
    	//创建线段树
        SegmentTreeNode *buildTree(int start,int end){
            if(start==end){
                return new SegmentTreeNode(start,end,nums_[start]);
            }
            int mid=start+((end-start)>>1);
            SegmentTreeNode *left=buildTree(start,mid);
            SegmentTreeNode *right=buildTree(mid+1,end);
            return new SegmentTreeNode(start,end,left->sum+right->sum,left,right);
        }
    	//更新线段树，将i处的值增加addval
        void updateTree(SegmentTreeNode *root,int i,int addval){
            if(root->start==i && root->end==i){
                root->sum+=addval;
                nums_[i]+=addval;
                return ;
            }
            int mid=root->start+((root->end-root->start)>>1);
            if(i<=mid){
                updateTree(root->left,i,addval);
            }else{
                updateTree(root->right,i,addval);
            }
            root->sum+=addval;
        }
    	//计算区间i到j的和
        int sumRange(SegmentTreeNode *root,int i,int j){
            if(root->start==i && root->end==j){
                return root->sum;
            }
            int mid=root->start+((root->end-root->start)>>1);
            if(i>mid){
                return sumRange(root->right,i,j);
            }else if(j<=mid){
                return sumRange(root->left,i,j);
            }else{
                return sumRange(root->left,i,mid)+sumRange(root->right,mid+1,j);
            }
        }
        /* 打印叶子节点，用于调试
        void printTree(SegmentTreeNode *root){
            if(root->left==nullptr && root->right==nullptr){
                cout<<root->sum<<" ";
                return ;
            }
            printTree(root->left);
            printTree(root->right);        
        }
        */
    private:
        vector<int> nums_;
        std::unique_ptr<SegmentTreeNode> root_;
    }; //end class NumArray

区间更新，单点查询

  • hdu 1556 Color the ball
    对于这类问题，算法的思想是在区间更新的时候不用全部实施到该区间的每个点上，只将该区间分为几部分，然后实施到分开的几个区间上就好。等到单点查询的时候将单点的值加上所有对该点的更新就好。
    由于对区间进行更新，所以二叉树每个节点上需要多一个updateval来维护对区间的更新。
    区间更新函数，跟上一类问题中的区间查询有点相似。
    单点更新：从根节点向下找到目标点，然后在回溯的时候直接加上每个每个包涵该点的区间维护的updateval。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    102
    103
    104
    105
    106
    107
    108
    109
    110
    111
    112
    #include <bits/stdc++.h>
    using namespace std;

    class SegmentTreeNode{
    public:
        SegmentTreeNode(int start,int end,int sum,int val=0,SegmentTreeNode *left=nullptr,SegmentTreeNode *right=nullptr):
                start(start),end(end),sum(sum),updateval(val),left(left),right(right) {}
        //禁用赋值构造和拷贝构造函数
        SegmentTreeNode(const SegmentTreeNode&)=delete;
        SegmentTreeNode& operator=(const SegmentTreeNode&)=delete;
        ~SegmentTreeNode(){
            delete left;
            delete right;
            left=right=nullptr;
        }
    public:
        int start;
        int end;
        int sum; //可以是max，min
        int updateval;  //用来记录当前区间上update过的数值
        SegmentTreeNode *left;
        SegmentTreeNode *right;
    }; //end class SegmentTreeNode

    class NumArray {
    public:
        NumArray(vector<int>& nums) {
            nums_.swap(nums);
            if(!nums_.empty()){
                root_.reset(buildTree(0,nums_.size()-1));
            }
        }
        void update(int s, int e, int val) {
            updateTree(root_.get(),s,e,val);
        }
        int query(int i) {
            return queryTree(root_.get(),i);
        }
    private:
    	//创建线段树
        SegmentTreeNode *buildTree(int start,int end){
            if(start==end){
                return new SegmentTreeNode(start,end,nums_[start]);
            }
            int mid=start+((end-start)>>1);
            SegmentTreeNode *left=buildTree(start,mid);
            SegmentTreeNode *right=buildTree(mid+1,end);
            return new SegmentTreeNode(start,end,left->sum+right->sum,0,left,right);
        }
    	//区间更新线段树，将区间s~e处的值增加addval
        void updateTree(SegmentTreeNode *root,int s,int e,int val){
            if(root->start==s && root->end==e){
                root->updateval+=val;
                return ;
            }
            int mid=root->start+((root->end-root->start)>>1);
            if(s>mid){
                updateTree(root->right,s,e,val);
            }else if(e<=mid){
                updateTree(root->left,s,e,val);
            }else{
                updateTree(root->left,s,mid,val);
                updateTree(root->right,mid+1,e,val);
            }

        }
    	//单点查询
        int queryTree(SegmentTreeNode *root,int i){
            if(root->start==i && root->end==i){
                return root->sum+root->updateval;
            }
            int mid=root->start+((root->end-root->start)>>1);
            if(i<=mid){
                return queryTree(root->left,i)+root->updateval;
            }else{
                return queryTree(root->right,i)+root->updateval;
            }
        }
    private:
        vector<int> nums_;
        std::unique_ptr<SegmentTreeNode> root_;
    }; //end class NumArray

    int main()
    {
        std::ios::sync_with_stdio(0);

        int N;
        int a,b;
        while(cin>>N){
            if(N==0) break;
            vector<int> tmp(N+1,0);
            NumArray numarry(tmp);
            for(int i=0;i<N;i++){
                cin>>a>>b;
                numarry.update(a,b,1);
            }
            if(N==1){
                cout<<numarry.query(1);
                return 0;
            }
            for(int i=0;i<N;i++){
                cout<<numarry.query(i+1);
                if(i!=N-1){
                    cout<<" ";
                }else{
                    cout<<endl;
                }
            }
        }
        return 0;
    }

区间更新，区间查询

  • 洛谷oj:P3372【模板】线段树1

  • 以下有两个版本,第一个是pushdown版本。
    添加pushdown()后，如果一个数列1~8，
    第一次更新1~4，就先将该操作实施到根节点的左孩子上就可以了(有的实现专门用个lazyflag标记，其实不用，如果updateval不为0，则说明lazyflag为1)，然后更新根结点的sum。
    如果第二次再更新3~4，在向下寻找线段3~4的过程中，要将之前的更新操作往下落实。于是就将1~4上的updateval清零，然后将该更新操作往下分别实施到1~2和3~4上。将寻找3~4的路径上的更新操作都落实到3~4上之后，再执行3~4的更新操作。然后回溯的过程中更新每个结点上的sum。
    在查询的时候，如果查询3~3区间，也是需要依次pushdown()，将之前的区间更新落实到3~3区间上，然后返回区间3~3那个结点的sum就可以了。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    102
    103
    104
    105
    106
    107
    108
    109
    110
    111
    112
    113
    114
    115
    116
    117
    118
    119
    120
    121
    122
    123
    124
    #include <bits/stdc++.h>
    using namespace std;

    class SegmentTreeNode{
    public:
        SegmentTreeNode(int start,int end,long long sum,long long val=0,SegmentTreeNode *left=nullptr,SegmentTreeNode *right=nullptr):
                start(start),end(end),sum(sum),updateval(val),left(left),right(right) {}
        //禁用赋值构造和拷贝构造函数
        SegmentTreeNode(const SegmentTreeNode&)=delete;
        SegmentTreeNode& operator=(const SegmentTreeNode&)=delete;
        ~SegmentTreeNode(){
            delete left;
            delete right;
            left=right=nullptr;
        }
    public:
        int start;
        int end;
        long long sum; //可以是max，min
        long long updateval;  //用来记录当前区间上update过的数值
        SegmentTreeNode *left;
        SegmentTreeNode *right;
    }; //end class SegmentTreeNode

    class NumArray {
    public:
        NumArray(vector<long long>& nums) {
            nums_.swap(nums);
            if(!nums_.empty()){
                root_.reset(buildTree(0,nums_.size()-1));
            }
        }
        void update(int s, int e, int val) {
            updateTree(root_.get(),s,e,val);
        }
        long long query(int s,int e) {
            return queryTree(root_.get(),s,e);
        }
    private:
    	//创建线段树
        SegmentTreeNode *buildTree(int start,int end){
            if(start==end){
                return new SegmentTreeNode(start,end,nums_[start]);
            }
            int mid=start+((end-start)>>1);
            SegmentTreeNode *left=buildTree(start,mid);
            SegmentTreeNode *right=buildTree(mid+1,end);
            return new SegmentTreeNode(start,end,left->sum+right->sum,0,left,right);
        }
    	//区间更新线段树，将区间s~e处的值增加addval
        void updateTree(SegmentTreeNode *root,int s,int e,int val){
            if(root->start==s && root->end==e){
                root->sum+=val*(e-s+1);
                root->updateval+=val;
                return ;
            }
            pushdown(root);
            int mid=root->start+((root->end-root->start)>>1);
            if(s>mid){
                updateTree(root->right,s,e,val);
            }else if(e<=mid){
                updateTree(root->left,s,e,val);
            }else{
                updateTree(root->left,s,mid,val);
                updateTree(root->right,mid+1,e,val);
            }
            root->sum=root->left->sum+root->right->sum;

        }
    	//区间查询
        long long queryTree(SegmentTreeNode *root,int s,int e){
            if(root->start==s && root->end==e){
                return root->sum;
            }
            pushdown(root);
            int mid=root->start+((root->end-root->start)>>1);
            if(e<=mid){
                return queryTree(root->left,s,e);
            }else if(s>mid){
                return queryTree(root->right,s,e);
            }else{
                return queryTree(root->left,s,mid)+queryTree(root->right,mid+1,e);
            }
        }
        void pushdown(SegmentTreeNode *root){
            if(root->updateval){
                root->left->updateval+=root->updateval;
                root->right->updateval+=root->updateval;
                int mid=root->start+((root->end-root->start)>>1);
                root->left->sum+=root->updateval*(mid-root->start+1);
                root->right->sum+=root->updateval*(root->end-mid);
                root->updateval=0;
            }
        }
    private:
        vector<long long> nums_;
        std::unique_ptr<SegmentTreeNode> root_;
    }; //end class NumArray

    int main()
    {
        std::ios::sync_with_stdio(0);

        long long n,m;
        long long tmp,oper,x,y,k;
        vector<long long> vi;
        cin>>n>>m;
        vi.resize(n+1);
        for(int i=1;i<=n;i++){
            cin>>vi[i];
        }
        NumArray numarry(vi);
        for(int i=0;i<m;i++){
            cin>>oper;
            if(oper==1){
                cin>>x>>y>>k;
                numarry.update(x,y,k);
            }else{
                cin>>x>>y;
                cout<<numarry.query(x,y)<<endl;
            }
        }
        return 0;
    }

  • 标记永久化版本，去掉了pushdown函数，比上一版本有一常数优化。
    pushdown版本的是每一次更新区间时，都顺带着将之前的更新向下落实。但是我们其实可以采取”区间更新，单点查询”时的做法，每次更新时实施到相应区间上，不用落实到最下面。然后在每次查询完，回溯的时候，把每个区间上的更新都加上。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    102
    103
    104
    105
    106
    107
    108
    109
    #include <bits/stdc++.h>
    using namespace std;

    class SegmentTreeNode{
    public:
        SegmentTreeNode(int start,int end,long long sum,long long val=0,SegmentTreeNode *left=nullptr,SegmentTreeNode *right=nullptr):
                start(start),end(end),sum(sum),updateval(val),left(left),right(right) {}
        //禁用赋值构造和拷贝构造函数
        SegmentTreeNode(const SegmentTreeNode&)=delete;
        SegmentTreeNode& operator=(const SegmentTreeNode&)=delete;
        ~SegmentTreeNode(){
            delete left;
            delete right;
            left=right=nullptr;
        }
    public:
        int start;
        int end;
        long long sum; //可以是max，min
        long long updateval;  //用来记录当前区间上update过的数值
        SegmentTreeNode *left;
        SegmentTreeNode *right;
    }; //end class SegmentTreeNode

    class NumArray {
    public:
        NumArray(vector<long long>& nums) {
            nums_.swap(nums);
            if(!nums_.empty()){
                root_.reset(buildTree(0,nums_.size()-1));
            }
        }
        void update(int s, int e, int val) {
            updateTree(root_.get(),s,e,val);
        }
        long long query(int s,int e) {
            return queryTree(root_.get(),s,e);
        }
    private:
    	//创建线段树
        SegmentTreeNode *buildTree(int start,int end){
            if(start==end){
                return new SegmentTreeNode(start,end,nums_[start]);
            }
            int mid=start+((end-start)>>1);
            SegmentTreeNode *left=buildTree(start,mid);
            SegmentTreeNode *right=buildTree(mid+1,end);
            return new SegmentTreeNode(start,end,left->sum+right->sum,0,left,right);
        }
    	//区间更新线段树，将区间s~e处的值增加addval
        void updateTree(SegmentTreeNode *root,int s,int e,int val){
            root->sum+=val*(e-s+1); //每次调用该函数，只有整棵线段树的根节点到目标结点的sum值会被更新
            if(root->start==s && root->end==e){
                root->updateval+=val;
                return ;
            }
            int mid=root->start+((root->end-root->start)>>1);
            if(s>mid){
                updateTree(root->right,s,e,val);
            }else if(e<=mid){
                updateTree(root->left,s,e,val);
            }else{
                updateTree(root->left,s,mid,val);
                updateTree(root->right,mid+1,e,val);
            }
        }
    	//区间查询
        long long queryTree(SegmentTreeNode *root,int s,int e){
            if(root->start==s && root->end==e){
                return root->sum;
            }
            int mid=root->start+((root->end-root->start)>>1);
            if(e<=mid){
                return queryTree(root->left,s,e)+root->updateval*(e-s+1);
            }else if(s>mid){
                return queryTree(root->right,s,e)+root->updateval*(e-s+1);
            }else{
                return queryTree(root->left,s,mid)+queryTree(root->right,mid+1,e)+root->updateval*(e-s+1);
            }
        }
    private:
        vector<long long> nums_;
        std::unique_ptr<SegmentTreeNode> root_;
    }; //end class NumArray

    int main(){
        std::ios::sync_with_stdio(0);

        long long n,m;
        long long tmp,oper,x,y,k;
        vector<long long> vi;
        cin>>n>>m;
        vi.resize(n+1);
        for(int i=1;i<=n;i++){
            cin>>vi[i];
        }
        NumArray numarry(vi);
        for(int i=0;i<m;i++){
            cin>>oper;
            if(oper==1){
                cin>>x>>y>>k;
                numarry.update(x,y,k);
            }else{
                cin>>x>>y;
                cout<<numarry.query(x,y)<<endl;
            }
        }
        return 0;
    }

区间最值模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
class SegmentTreeNode2{
public:
    SegmentTreeNode2(int start,int end,int max,int min,
                    SegmentTreeNode2 *left=nullptr,SegmentTreeNode2 *right=nullptr):
            start(start),end(end),maxx(max),minn(min),left(left),right(right) {}
    //禁用赋值构造和拷贝构造函数
    SegmentTreeNode2(const SegmentTreeNode2&)=delete;
    SegmentTreeNode2& operator=(const SegmentTreeNode2&)=delete;
    ~SegmentTreeNode2(){
        delete left;
        delete right;
        left=right=nullptr;
    }
public:
    int start;
    int end;
    int maxx;
    int minn;
    SegmentTreeNode2 *left;
    SegmentTreeNode2 *right;
}; //end class SegmentTreeNode2

class NumArray {
public:
    NumArray(vector<int>& nums) {
        nums_.swap(nums);
        if(!nums_.empty()){
            root_.reset(buildTree(0,nums_.size()-1));
        }
    }
    int getMax(int i, int j) {
        return getMax(root_.get(),i,j);
    }
    int getMin(int i,int j){
        return getMin(root_.get(),i,j);
    }
private:
	//创建线段树
    SegmentTreeNode2 *buildTree(int start,int end){
        if(start==end){
            return new SegmentTreeNode2(start,end,nums_[start],nums_[start]);
        }
        int mid=start+((end-start)>>1);
        SegmentTreeNode2 *left=buildTree(start,mid);
        SegmentTreeNode2 *right=buildTree(mid+1,end);
        return new SegmentTreeNode2(start,end,max(left->maxx,right->maxx),min(left->minn,right->minn),left,right);
    }

    int getMax(SegmentTreeNode2 *root,int i,int j){
        if(root->start==i && root->end==j){
            return root->maxx;
        }
        int mid=root->start+((root->end-root->start)>>1);
        if(i>mid){
            return getMax(root->right,i,j);
        }else if(j<=mid){
            return getMax(root->left,i,j);
        }else{
            return max(getMax(root->left,i,mid),getMax(root->right,mid+1,j));
        }
    }
    
    int getMin(SegmentTreeNode2 *root,int i,int j){
        if(root->start==i && root->end==j){
            return root->minn;
        }
        int mid=root->start+((root->end-root->start)>>1);
        if(i>mid){
            return getMin(root->right,i,j);
        }else if(j<=mid){
            return getMin(root->left,i,j);
        }else{
            return min(getMin(root->left,i,mid),getMin(root->right,mid+1,j));
        }
    }

private:
    vector<int> nums_;
    std::unique_ptr<SegmentTreeNode2> root_;
}; //end class NumArray


class Solution {
public:
    /**
     * @param num: array of num
     * @param ask: Interval pairs
     * @return: return the sum of xor
     */
    int Intervalxor(vector<int> &num, vector<vector<int>> &ask) {
        // write your code here
        NumArray na(num);
        int res=na.getMax(ask[0][0]-1,ask[0][1]-1)+na.getMin(ask[0][2]-1,ask[0][3]-1);
        for(int i=1;i<ask.size();i++){
            res^=(na.getMax(ask[i][0]-1,ask[i][1]-1)+na.getMin(ask[i][2]-1,ask[i][3]-1));
        }
        return res;
    }
};

参考